Productos notables

 PRODUCTOS NOTA

EVALUACIÓN PRODUCTOS NOTABLES 

https://quizizz.com/join?gc=626171&source=liveDashboard

Cuadrado de un binomio

EJEMPLOS:

BINOMIO CONJUGADO

 NÚMEROS REALES

Qué son los números reales

Cuando se definen los números reales se dice que son cualquier número que se encuentre o corresponda con la recta real que incluye a los números racionales y números irracionales, Por lo tanto, el dominio de los números reales se encuentra entre menos infinito y más infinito.

Una vez revisados los anteriores conjuntos de números existentes, podemos decir que el conjunto de los números reales (R$\mathbb{<br>}$) está integrado por:

• El conjunto de los números racionales (Q$\mathbb{<br>}$) que corresponden a la unión de todos los números cuya expresión decimal es finita o infinita periódica.
• El conjunto de los números irracionales (I$\mathbb{<br>}$) que está formado por la unión de todos los números que admiten una expresión infinita no periódica.

Entonces, se llaman números reales a todos aquellos que se pueden expresar en forma decimal finita o infinita; es decir, el conjunto de los números reales (R$\mathbb{<br>}$) está formado por los elementos del conjunto Q$\mathbb{<br>}$ unido con I$\mathbb{<br>}\mathbb{<br>}\mathbb{<br>}$

NUMEROS IRRACIONALES

PRODUCTO CARTESIANO Y SUS RELACIONES 

El producto cartesiano revela una relación de orden entre dos conjuntos, constituyéndose como un tercer conjunto. El producto cartesiano de un conjunto A y de un conjunto B es el conjunto constituido por la totalidad de los pares ordenados que tienen un primer componente en A y un segundo componente en B.

Relaciones

Diagrama de Venn Relación Notación. R es una relación de A en B, también se denota por R: A → B 2. Si el par (x, y) pertenece a la relación R, se acostumbra a denotar por (x, y) ∈ R  ,  x R y  ,  y = R(x)

Definición Relación Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamado Recorrido o Rango, de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango. Toda relación queda definida si se conoce el conjunto de partida, el conjunto de llegada y la regla mediante la cual se asocian los elementos La relación es subconjunto del Producto Cartesiano, los pares ordenados que la forman cumplen “Una condición específica”

GeoGebra

https://www.geogebra.org/classic#3d

TEOREMA DE PITAGORAS

 

TEOREMA DE PITAGORAS

Es una fórmula, proveniente de la Geometría Euclidiana denominada así en honor al matemático griego Pitágoras, que establece una relación entre los 3 lados de un triángulo rectángulo. Es decir, conocidos dos de ellos es posible calcular el otro con esta ecuación.

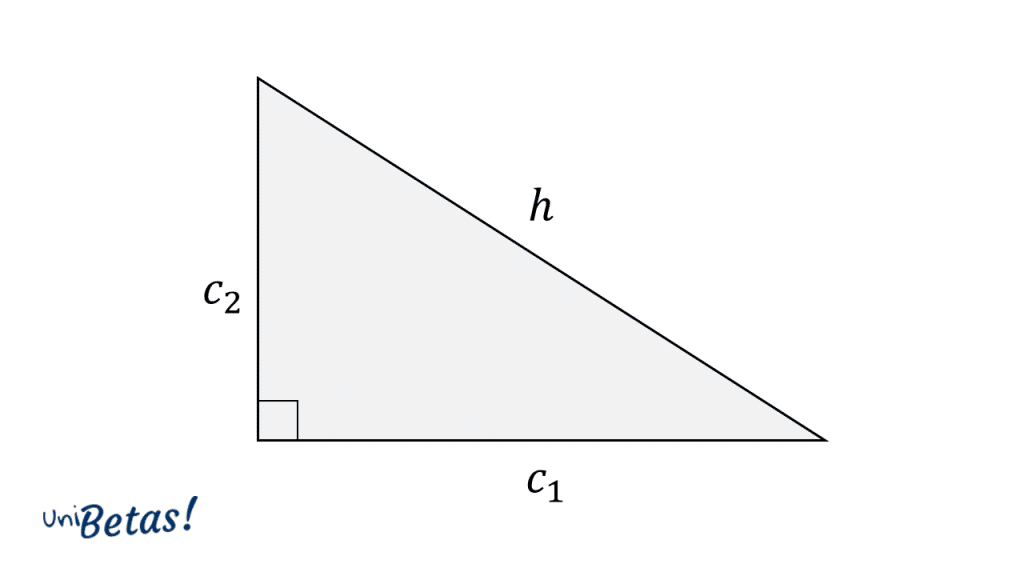
La definición formal del Teorema de Pitágoras establece que:

El cuadrado de la hipotenusa h de un triángulo rectángulo cualquiera, es igual a la suma del primer cateto 1 al cuadrado más el segundo cateto 2 también al cuadrado.

Escrito en lenguaje algebraico, esta relación quedaría como:

${ℎ}^2={{�}^2}_1+{{�}^2}_2$

Donde ${�}_1$ y ${�}_2$ son los catetos del triángulo rectángulo. Otra forma de interpretar al Teorema de Pitágoras, es a través de las áreas que forman los cuadrados representados por cada uno de los lados del triángulo rectángulo.

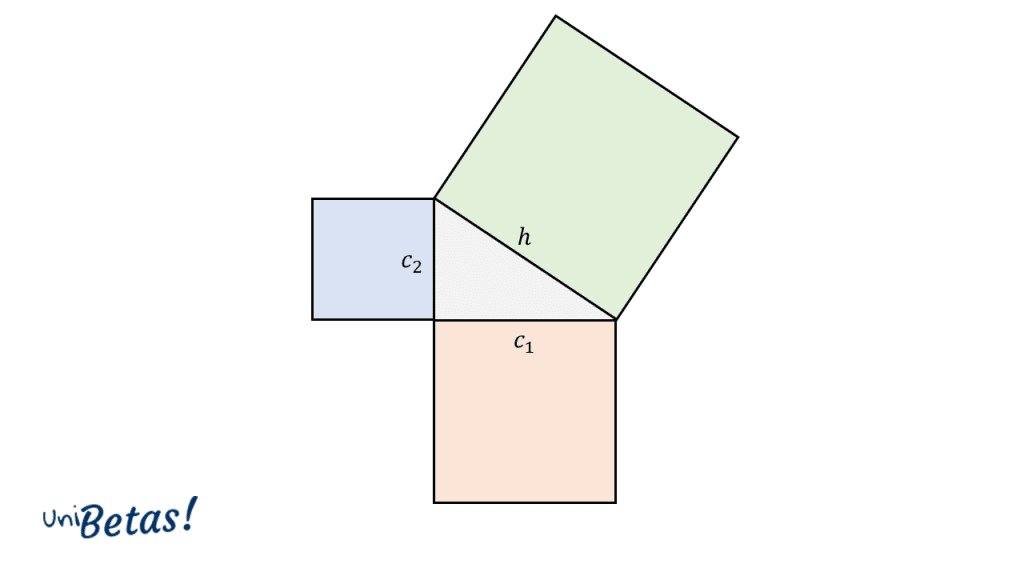
Si a cada uno de los lados del triángulo rectángulo lo asociamos con el lado de un cuadrado, la ecuación del Teorema de Pitágoras nos diría que: el área del cuadrado de lado $ℎ$ es igual a la suma de las áreas de los cuadrados de lado ${�}_1$ y ${�}_2$.

0

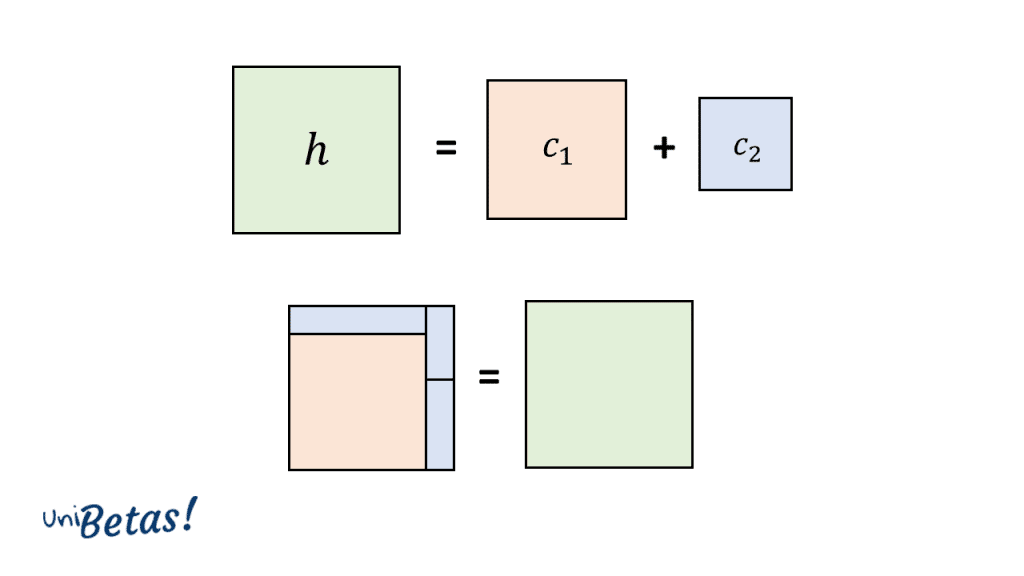
EXPRESIONES ALGEBRAICAS - LENGUAJE ALGEBRAICO

 EXPRESIONES ALGEBRAICAS

¡Mira este video para entender un poco más! Observa la siguiente expresión:

LENGUAJE ALGEBRAICO

 

¿Qué es un lenguaje algebraico?

El lenguaje algebraico es el lenguaje de las matemáticas. Es decir, a un sistema de expresión que emplea símbolos y números para expresar aquello que usualmente comunicamos mediante palabras, y que nos permiten formular teoremas, resolver problemas y expresar proporciones o relaciones formales de distinta naturaleza.

¿Para qué sirve un lenguaje algebraico?

Como hemos dicho antes, el lenguaje algebraico sirve para construir expresiones algebraicas, es decir, formulaciones en las que números, símbolos y letras se combinan para expresar una relación lógica y/o formal, en la que algunas cantidades se conocen y otras son desconocidas.

Fuente: https://concepto.de/lenguaje-algebraico/#ixzz8N76mYA4m

Ingresar¡Crea tu cuenta!

Álgebra -

 

Expresiones algebraicas

Ir al cu

CONJUNTOS

 CONJUNTOS

Un conjunto es la agrupación de diferentes elementos que comparten entre sí características y propiedades semejantes. Estos elementos pueden ser sujetos u objetos, tales como números, canciones, meses, personas, etc. Por ejemplo: el conjunto de números primos o el conjunto de planetas del sistema solar.

DIAGRAMA DE VENN

OPERACIONES CON CONJUNTOS 

Triángulos y su construcción 

Ángulos

Un triángulo es una figura geométrica plana que tiene tres lados, tres vértices y tres ángulos. Los triángulos son los polígonos más simples que existen y carecen de diagonal, ya que con tres puntos no alineados cualesquiera es posible formar un triángulo. La suma de los ángulos interiores de un triángulo siempre es igual a 180°1. Los triángulos se clasifican según la longitud de sus lados y la medida de sus ángulos. A continuación, se presentan los tipos de triángulos más comunes:

• Triángulo equilátero: Es aquel que tiene los tres lados iguales y los tres ángulos internos iguales a 60°1.
• Triángulo isósceles: Es aquel que tiene dos lados iguales y dos ángulos internos iguales1.
• Triángulo escaleno: Es aquel que tiene los tres lados y los tres ángulos internos diferentes1.

Además, los triángulos pueden ser clasificados según la medida de sus ángulos internos:

• Triángulo acutángulo: Es aquel que tiene todos sus ángulos internos agudos (menores a 90°)1.
• Triángulo rectángulo: Es aquel que tiene un ángulo interno recto (igual a 90°)1.
• Triángulo obtusángulo: Es aquel que tiene un ángulo interno obtuso (mayor a 90°)1.